My work project started pretty simple: there was a simple GetXyz endpoint that just looked up the xyz record in the database by a unique key & returned it. How complicated could it be?

It was a straightforward generalization of an old GetAbc functionality, it was really only used by oncall engineers through an admin console, it shouldn’t have been too big of a deal.

Ok, but then it outgrew its original datastore, so a separate service had to be created. We thought about migrating clients, but at the time it seemed faster to just implement once on our side & have clients continue calling us; essentially encapsulating the separate service as an implementation detail. But as part of the traffic swing, we figured it should support either the local or the remote read path.

I have this “American Express Blueprint Business Loan” product to have a line of credit for the rentals if I’m ever in a pinch.

They allow up to $21,700 with this very easy application process, you basically just slide a slider to the amount needed & select between 6, 12, 18, 24 months:

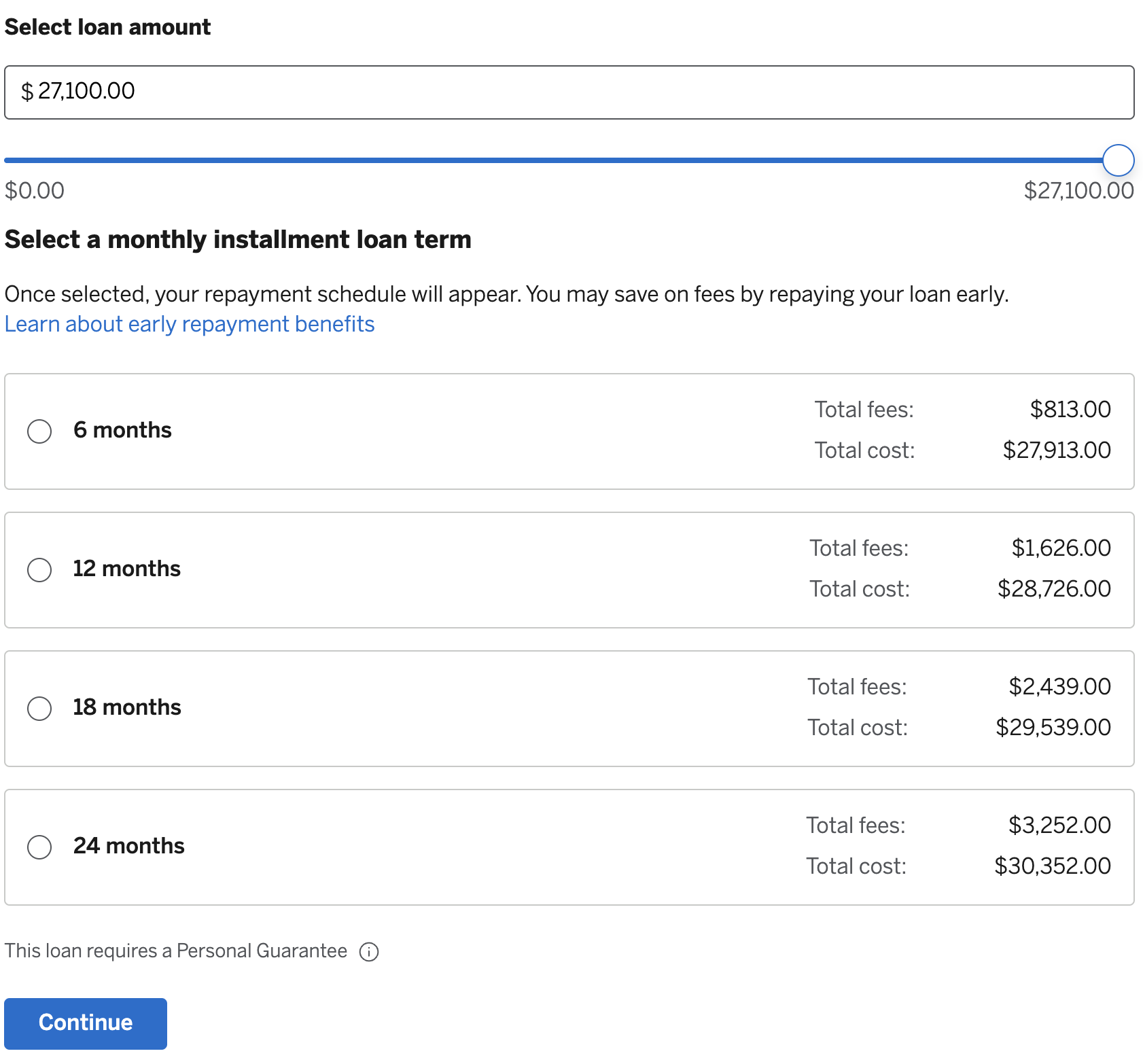
This shows a schedule like this:

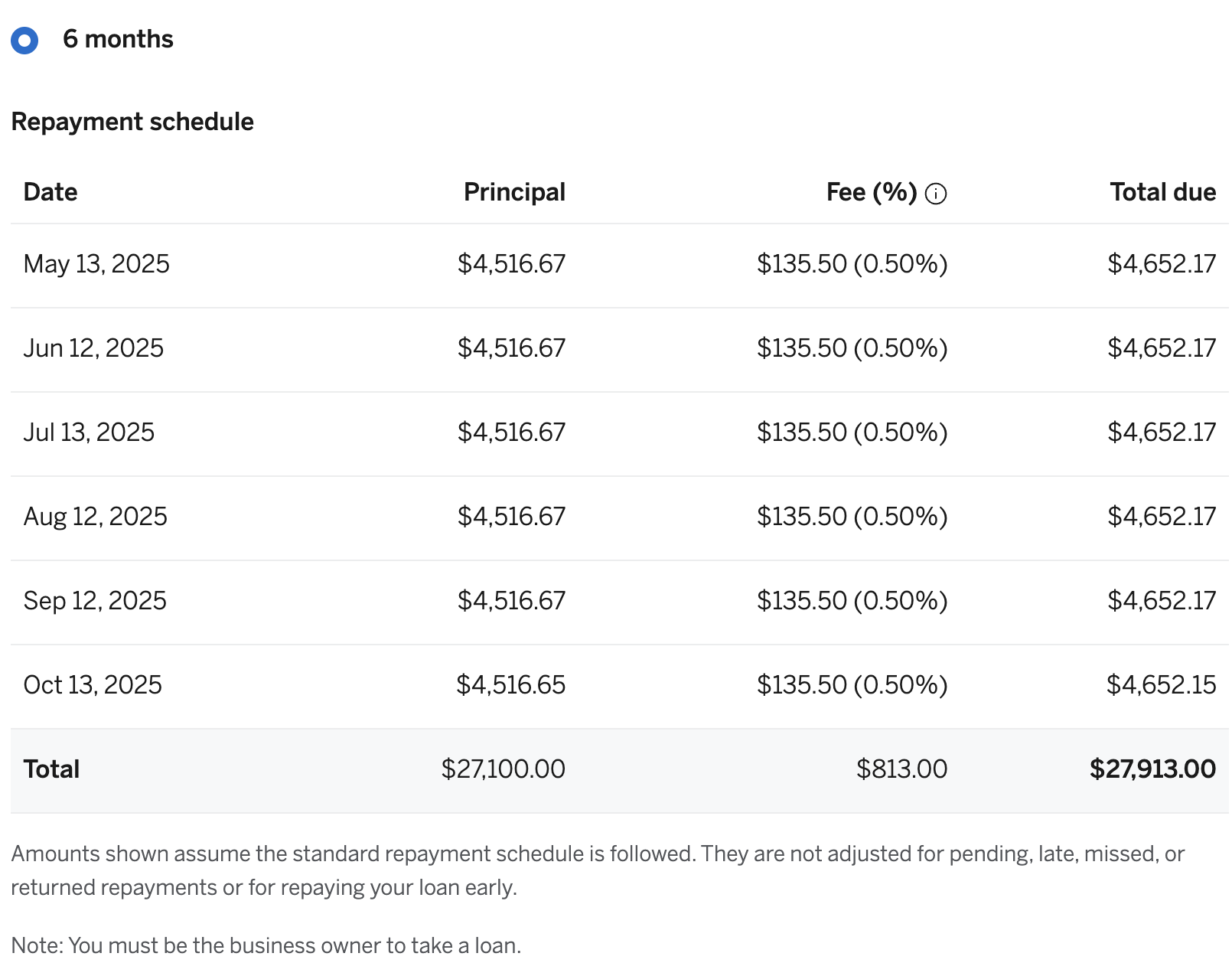
Looking at this, there’s a lot of temptation to think

It’s been a while since I’ve written an update – 2.5y! – and a long time since I wrote very frequently. On top of all the crazy ways the world has changed in the last five years, a bunch has changed for me personally in the last five years as well, along a bunch of different axes.

I think part of the reason it’s been hard to post is wanting to avoid coming across as bragging about the high points of this journey and also not really wanting to admit some of the low points, but I feel I’ve had a lot on my mind that doesn’t really make sense in blog form without the greater context; I’ve decided that I’d rather just share a lot of what’s been going on in the hopes that some part of it is relevant to someone out there or gives them some fortitude for whatever low spot they’re going through or can learn something from it.